A foundation or face primer is a cream or lotion that is applied before a liquid or powder foundation is applied to create a base for applying makeup.Most Indian makeup brands have not yet come up with a face primer so I never used one before, but since everyone was raving about it I thought I’ll give it a shot.I did find a couple of primers available online and a few how to videos on you tube.The do it yourself version seemed simple with easily available ingredients not too mention cheap so I tried it out and voila was I impressed or what.Since I’ve not actually tried a pre-packaged primer I won’t be able to compare it to one but it did meet and fulfill all the requirements of a face primer.

A face primer works by creating a canvas for makeup to set on.Other benefits include:
Here's my version of a homemade face primer.
Hunt And Collect:

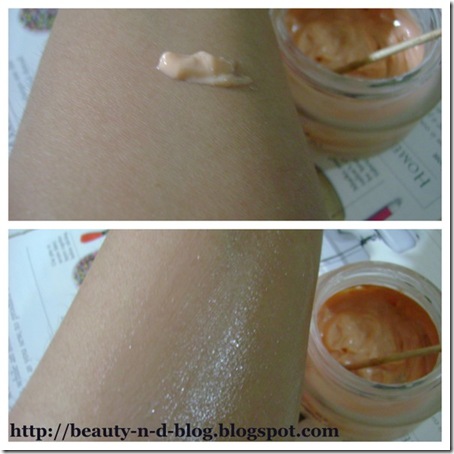
The concoction will work primarily as a face primer but it can double up as a tinted moisturizer too which is exactly how I’ve been using it.You could add a touch of a pearlescent eye shadow/pigment to turn it into a highlighting cream too.The possibilities are numerous just put your head to it and let me know how it turns out.

A face primer works by creating a canvas for makeup to set on.Other benefits include:
- Even out skin tone
- Fill in tiny lines and pores which are sometimes highlighted by other products
- Helps makeup stay longer (especially in hot weather)
- Absorb excess oil
Here's my version of a homemade face primer.
Hunt And Collect:
- Aloe Vera gel
Don’t use fresh gel as that might turn rancid.Use the pre-packaged version.You can buy it at any medical store.This will provide the base for the primer.If you have oily skin you might want to increase the amount of aloe gel.Normally aloe Vera suits everyone but occasionally it doesn't.Unfortunately in that case you won’t be able to make this primer.If anyone has an alternative for the aloe Vera do let me know.
- Water Based Moisturizer
Since the most important function of a primer is to keep oil at bay I would strongly suggest using a water based moisturizer.I’m using Oriflame Giordani Gold Body Cream.I know not even in the vicinity of a water based moisturizer but these days I have really dry skin and this cream is all I’m using.Plus it has this amazing fragrance which totally kick starts my mornings.Lacto Calamine (review here) would also work for the purpose but it might be a little too runny.So adjust the formula accordingly.I have used both.If you have dry skin you can increase the quantity of the moisturizer(or use a regular moisturizer like me).
- Sunscreen
Totally optional but since I hate applying product over product, adding sunscreen to the primer makes sense.Again try using a water based sunscreen with preferably a high SPF since we will add only a small amount.I’m using Avon Smooth UV Gel with SPF 20(Missing from the picture because I remembered it after clicking everything and it was too much bother to do it all over again).
- Liquid Foundation
Again optional.My reason for adding it is to make the primer work as a tinted moisturizer too, so that I can skip foundation when I don’t want to OD on makeup.However since my main motive here is to dupe a primer I compromise on it’s tinting/coverage quality.Normally a few drops is all I need.I’m using Maybelline Wonder Finish Liquid To Powder Foundation.
- Loose Powder
The aloe gel will give the primer it’s base and the powder will help to give the mattifying effect.You can use tinted face powder or a compact(scrape it out using a nail filer) or baby powder would work too.Make sure you don’t add a lot or the mixture will not come together.I’m using Lakme Rose Powder(review here) which is tinted and thus will add a base to the primer along with the foundation.
- A container for storage
The primer can easily be stored for a couple of weeks so you don’t have to concoct this every time you want to apply.I've used an empty cream container.Make sure it’s clean and dry.It can also double up as your mixing bowl.Get To Work:

- Start off with a 1 : 1 ratio of aloe gel and moisturizer.If you have an oily skin you could change the ratio to 1.5 : 1 or if you have dry skin you could change it to 1 : 1.5
- Add a pea-sized blob of sunscreen.
- Add a few drops of the liquid foundation.
- Add a couple of pinches of loose powder.
- Blend everything up using a spatula or wooden spoon.You should get an even consistency, not too runny which means you have either added too much moisturizer or foundation.You can balance out the consistency by adding more aloe gel and loose powder.
- Scrape off any excess from the sides and you are done.I prefer storing it in the fridge to cool it so it feels refreshing when I apply in the morning.

The concoction will work primarily as a face primer but it can double up as a tinted moisturizer too which is exactly how I’ve been using it.You could add a touch of a pearlescent eye shadow/pigment to turn it into a highlighting cream too.The possibilities are numerous just put your head to it and let me know how it turns out.
Oh my god! I love you for doing this post. I've been looking for such a recipe for the longest time! Will try it right away!
ReplyDelete@ Burcin: Thanks sweetie.Do let me know how it turns out :)
ReplyDeleteHey Sonia!
ReplyDeleteI did a post about homemade face primer and wanted to let you know how it went. Not trying to advertise or anything. You can delete the post later if u want!
http://lalebeauty.blogspot.com/2011/07/trying-out-homemade-face-primer.html
That's great.I'm happy that the dupe worked for you.
ReplyDeleteawesum........this post is very helpful:)
ReplyDeleteLove this post!!! Io like it that you use gel base instead of cream. Will surely try this out. Maybe we can also try adding something that mattifies the skin too.
ReplyDelete@Sudha:Like what?
ReplyDeleteawesome stuff - will do it soon ... n wont end up spending a fortune on costly primer ... thnks :)
ReplyDelete@Prachi:You're welcome sweety :)
ReplyDeleteI'm new to blogging please join my blog and spread the word ... thank you :)
ReplyDeletehere is the link -http://beautynindulgence.blogspot.com/
Do you think a mineral powder foundation would work in lieu of liquid foundation and powder?
ReplyDelete@Anonymous:Will do :)
ReplyDeletethis is awesoem..i will try it this weekend sonia...ty so much for this beautiful post
ReplyDelete@Pavani: You're welcome hon, let me know how it fares :)
ReplyDeletei cant wait to try this i have really oily skin and all the other diy primers use vaseline!!!not good for me im going to put rice powder instead of loose powder they say its super good for absorbing oil thnks for the post
ReplyDelete@Anonymous: Vaseline on face might just spell disaster.Rice powder sounds like a nice substitute.Next time will definitely give it a shot.
ReplyDeletehi.. i dont want to add foundation, is the loose powder necessary or can i carry on with the aloe vera gel and moisturiser only??
ReplyDeleteby z way great post :)
@Anonymous: Of course, the foundation is just to give the primer a tint.You can also use aloe gel on it's own.I have tried it and it worked just as great.
ReplyDeleteAnd thanks I'm glad you found the post useful.
Awesome! But, wouldn't mixing foundation, etc. to the aloe gel absorb in to the pores with the aloe gel? I moisturizer with Solar SPF 30. Www.devita.net, after MUCH research and then use a primer to keep everything else out if my pores. BTW, Clarsonuc's deep pore cleansing brush REALLY gets it all out! I love the idea of an aloe primer and will experiment with my SPF/moisturizer. Thanks!!
ReplyDelete@Anonymous:Nope the aloe vera acts as a barrier between the skin and foundation.Heard a lot of good things about the clarisonic, haven't tried it though!
ReplyDeleteI don't have any loose powder. What can I do?
ReplyDeletebaby powder
Delete